
1. Descrizione della tecnica
Questa tecnica di analisi dei dati, come del resto molte altre, più che un metodo da seguire analiticamente è un “metodo di ragionamento” che serve ad estrarre i dati davvero significativi su cui concentrare le nostre azioni. Esso parte dal concetto che, in molti processi, un numero limitato di cause produce la maggior parte degli effetti (di conseguenza: un numero grande di cause produce un numero limitato di effetti).

Una definizione precisa si trova nel manuale di statistica di Levine, Krehbiel, Berenson:"Il principio di Pareto si verifica quando la maggioranza delle osservazioni è caratterizzata da un numero esiguo di modalità—dette le “poche modalità rilevanti” - e le poche osservazioni rimanenti si disperdono su un gran numero di modalità—dette le “molte modalità banali”. In questa definizione viene utilizzato un linguaggio tipico della statistica. Per “osservazioni” si intendono gli “effetti osservati”, mentre con il termine “modalità” si intendono le “cause”. Con qualche esempio pratico sicuramente questo concetto apparirà più chiaro.
ESEMPIO 1: una piccola azienda meccanica vuole individuare quali sono i motivi (“CAUSE”) per i quali si ha un alto numero di servomotori difettosi (“EFFETTO”). In fase di prova vengono date delle schede che gli operatori addetti al controllo devono riempire segnalando, per ogni pezzo difettoso trovato, la causa della difettosità.
| MOTIVO | QUANTITA' | PERCENTUALE |
|---|---|---|
| Scatola danneggiata | 53 | 4.44% |
| Albero danneggiato | 35 | 2.93% |
| Gioco assiale | 130 | 10.9% |
| Attrito | 275 | 23.05% |
| Alta tensione scarsa | 43 | 3.6% |
| Voltaggio iniziale alto | 191 | 16.1% |
| Stampaggio sbagliato | 108 | 9.05% |
| Bassa velocità | 97 | 8.13% |
| Circuito aperto | 29 | 2.43% |
| Corsa massima | 58 | 4.87% |
| Assemblaggio sbagliato | 174 | 14.59% |
Se analizziamo questi dati possiamo verificare che più della metà dei pezzi difettosi sono dovuti a solo tre cause. I tecnici dunque, invece che disperdere energie su cause trascurabili, possono concentrarsi inizialmente solo su questi tre problemi in modo da ridurre a meno della metà la percentuale di difettosità. In seguito si potrà procedere ad eliminare anche gli altri problemi. Naturalmente questo è un classico esempio di processo di produzione industriale. La stessa tecnica si può però usare nei campi più disparati. Vediamo dunque un altro esempio applicato ad un problema di tipo “commerciale”.
ESEMPIO 2: Il nuovo Direttore Commerciale di un’azienda che produce abbigliamento vuole compiere personalmente una qualche azione sui Clienti. Questi ultimi sono però un migliaio e difficilmente riuscirebbe a portare a termine il proprio compito entro i termini stabiliti. A questo punto si fa stampare l’elenco dei clienti con accanto il fatturato fatto con essi nell’ultima stagione. In breve scopre che basta agire su circa il 30% dei clienti per coprire ben il 70% del fatturato.
Su internet si possono trovare molti esempi come quelli qui di seguito "generici":
Nell’elenco vengono utilizzate le percentuali 20—80 ma è ovvio che queste possono variare a secondo del caso, anche in modo importante.
Perché accade questo? Perché in molti processi si osserva questo principio? E’ semplicemente un fatto statistico. Senza scendere in dimostrazioni piuttosto noiose si può arrivare a capirne il motivo riflettendo su qualcosa di molto semplice. Supponiamo di avere 8 palline e un percorso di tubicini entro cui queste palline possono scorrere. Il percorso è una struttura ad albero rovesciato, perfettamente simmetrica.

Le palline scelgono il percorso in modo del tutto casuale. Alla fine di ogni percorso c’è un contenitore.Cominciamo a infilare le palline nel percorso e vediamo quello che accade. Ripetiamo varie volte l’esperimento. Intuitivamente, quante probabilità abbiamo (rispetto a tutte le possibili configurazioni) che alla fine dell’esperimento ogni contenitore contenga una sola pallina? Molto poche. ;Nel caso in figura ad esempio, si può osservare che “il caso” ha portato ad avere che due contenitori ( 25% del totale) contengono 5 palline (62% del totale).

Si può obbiettare che, anche se improbabile, la configurazione “ogni contenitore contiene una sola pallina” può verificarsi e per essa non vale il principio di Pareto. Giusto. E’ per questo motivo che ho riportato la definizione di un libro di statistica. Rileggiamola: “il Principio di Pareto si verifica quando…..” non dice: “in un qualunque processo le osservazioni rilevanti…..”.;Per curiosità ho calcolato la probabilità di avere una pallina per ogni contenitore. Nel caso di 5 palline e 5 contenitori la probabilità è del 1.46%.
Quando si vuole utilizzate il Principio di Pareto in modo analitico, è molto utile ricorrere ad un diagramma. Ad esempio, consideriamo il magazzino delle materie prime di un’officina meccanica. Con un software gestionale è facile tirar fuori la quantità movimentata per ognuno dei codici presente in magazzino. Mettiamo questo elenco in ordine decrescente di movimentazione. Calcoliamo quindi la percentuale di movimentazione di ognuno di essi sul totale movimentato. Otteniamo un qualcosa del genere:

Si può costruire un grafico in cui possiamo riportare sulle ascisse i codici dei materiali presenti in magazzino, e sulle ordinate la PERCENTUALE CUMULATA delle quantità movimentate. Per percentuale cumulata si intende, nel nostro caso, che al codice “0012” corrisponde la percentuale 35%, al codice “0014” la percentuale 35%+25%, al codice “0019” la percentuale 35%+25%+15%, e così via. Otteniamo così:

Possiamo ora suddividere il grafico in tre zone chiamate rispettivamente “A”, “B”, “C”. .
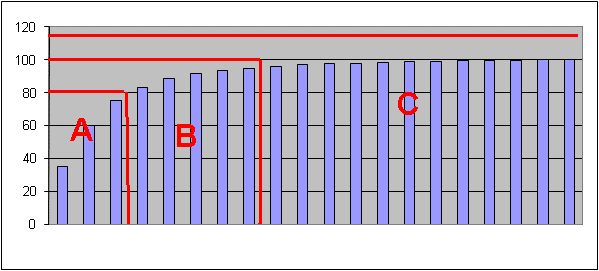
Nella zona “A” racchiudiamo i codici che coprono circa l’80% della movimentazione. Nella zona “B” racchiudiamo invece i codici che complessivamente hanno una movimentazione del 15% circa del totale. Nella zona “C” lasciamo invece i codici a scarsa movimentazione e che rappresentano in totale il 5%. Con un’analisi del genere è facile dunque individuare quale deve essere la distribuzione delle scorte da avere in magazzino. Soprattutto sappiamo che avendo in magazzino una sufficiente scorta dei codici racchiusi nella zona “A” , pur essendo quest’ultimi in numero limitato, riusciamo a far fronte all’80% delle necessità.